The Knot System

The Sequential System

For centuries, humans have sought methods to describe relationships. The most common practice is to assign names to the kinships, such as father, mother, sister, brother, uncle, niece, grandfather etc. However, these verbal terms do not define consanguinity precisely enough for maximum scientific use.

Geneticists and genealogists need a system that permits them to comprehend more complex relations than those traditionally possible. Sir Francis Galton (1822-1911) stated the problem more than a century ago in a letter to the editor of Nature, concerning an Arithmetic Notation of Kinship:

Many writers have endeavoured to devise a simple method of describing the various forms of kinship, which, when expressed verbally, are cumbrous and puzzling in the highest degree. I suspect, however, that if we had always been as familiar with the binary system of arithmetic as we are with the decimal, that the facilities afforded by a numerical system of notation of kinship would have been so obvious that it would have been adopted as a matter of course.

Galton's letter briefly discusses the sequential numbering scheme for ancestors now known by European genealogists as the Kekule von Stradonitz System and by North American genealogists as the Stradonitz or Ahnentafel System. However, the plan was invented by neither Sir Francis Galton nor Stephen Kekule von Stradonitz (1863-1933). The latter's name is attached to it because he was the first to describe its properties (in 1898).

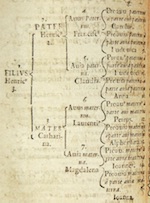
The first printed version of this arrangement dates back to 1590, when an Austrian historian and diplomat, Michael Eyzinger (Michael von Aitzing, 1530-1598), used it in his book on European princely and royal houses. The scheme is so simple and logical that many genealogists since then have used it without knowledge of predecessors and even without considering it in need of explanation. On this homepage the method is referred to as the Sequential System.

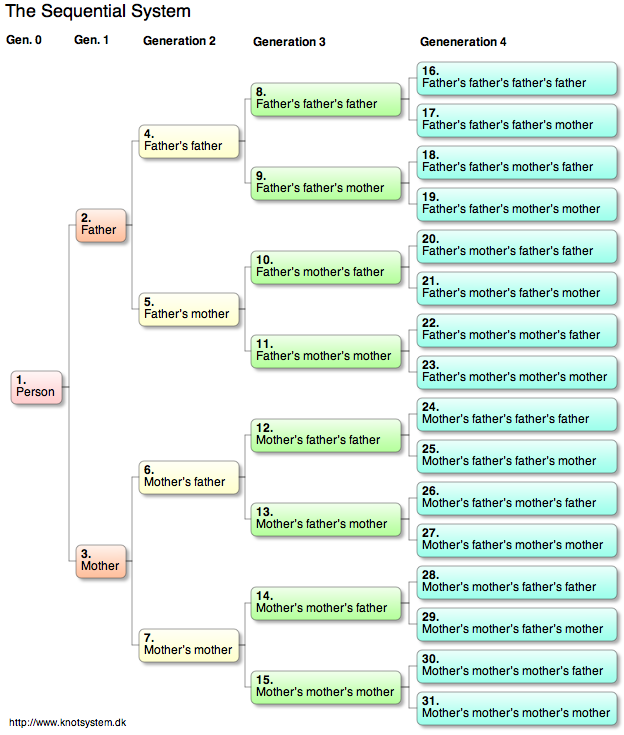
The Sequential System

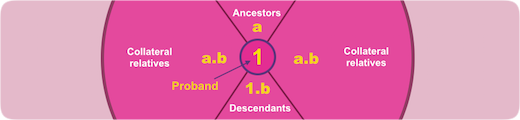
Widely accepted as the preferred notation for documentation and exchange of genealogical research data about ancestors, its plan is simple. Consecutive integers (whole numbers) are assigned to all ancestors of a person - 1 to the person, 2 to the father, 3 to the mother, 4 to the father's father, etc.

Because each person has a countable number of ancestors and there exists an infinite number of integers, it is possible to assign a correct number to any ancestral position, even if some positions remain unidentified. Because of the inherent binary structure of bisexual procreation, many properties may be derived directly from this numbering plan.

Properties of the Sequential System

Gender
Male ancestral positions have even numbers; female ancestral positions have odd numbers.

Parents
The father of any ancestor n has number 2n, and the mother has number 2n + 1.

Offspring
The offspring position of any ancestor n is calculated as the integer part of n/2.

Mate
A male ancestor n's mate has number n + 1, and a female ancestor n's mate has number n - 1.

Relationship
The exact relationship between any ancestor n and the individual at position 1 is calculated by successively dividing n by 2, discarding fractions at each stage, until reaching the number 1. The resulting list of integers identifies the ancestral positions that form the lineage. The number of times that n is halved equals the number of generations between the individual and the ancestor at position n.

Ancestors per generation
The first ancestor number in every generation (1, 2, 4, 8, 16, etc.) corresponds to the number of ancestor positions in that generation.

Generation numbers
Above ancestor numbers are also exponentiations of 2 (i.e., 2⁰, 2¹, 2², 2³, 2⁴, etc.), and the exponent may be used as the generation number (i.e., 2⁴ - or, 2 to the fourth power - represents the fourth ancestral generation).

Relationship type
Pure male (agnatic) ascent from an individual exists for ancestor position numbers which are a power of 2 (2, 4, 8, . .).
Pure female ascent exists for ancestor position numbers which are power of 2 minus 1 (3, 7, 15, . . ).

Generation number	Pure male  ascent	Ancestor pos. father's side	| |	Ancestor pos. mother's side	Pure female ascent
n	2n		|		2n+1 - 1
15	32,768	32,768 - 49,407	|	49,408 - 65,535	65,535
14	16.384	16,384 - 24,703	|	24,704 - 32,767	32,767
13	8,192	8,192 - 12,351	|	12,352 - 16,383	16,383
12	4,096	4,096 - 6,175	|	6,176 - 8,191	8,191
11	2,048	2,048 - 3,087	|	3,088 - 4,095	4,095
10	1,024	1,024 - 1,543	|	1,544 - 2,047	2,047
9	512	512 - 771	|	772 - 1,023	1,023
8	256	256 - 385	|	386 - 511	511
7	128	128 - 191	|	192 - 255	255
6	64	64 - 95	|	96 - 127	127
5	32	32 - 47	|	48 - 63	63
4	16	16 - 23	|	24 - 31	31
3	8	8 - 11	|	9 - 15	15
2	4	4 - 5	|	6 - 7	7
1	2	2	|	3	3
0			1
		Proband